Energy-Based Models (EBMs)이란? (1) - 개념, training, sampling - 웅 공부방

 

Energy-based generative Models이 나오기 이전에도 Autoregressive models, Normalizing flow models, Variational autoencoders(VAE), GANs 등 많은 generative mode이 존재했다. 다만, 이 모델들은 모두 치명적인 단점을 갖고 있다. Autoregressive models, Normalizing flow models, VAE들은 likelihood $P_{\theta}$를 모델링하는 데 있어 각각 특정 콘셉트를 가지고 있기에 선택할 수 있는 model architectures가 제한적이다.

 

예를 들어 Autoregressive models는 chain rule을 이용하여 conditionals의 곱으로 likelihood를 정의하고 있다. 이를 식으로 나타내면 다음과 같다.

 

$$P_{\theta }(\mathbf{x})=\prod _{i=1}^{n}P({\mathbf{x}}_i|{\mathbf{x}}_{<i})$$

 

Autoregressive models를 만들 때, $\mathbf{x}$에 대한 likelihood 값이 첫 번째 차원부터 마지막까지 conditionals의 곱이 되도록 모델링해야 한다. GANs 같은 경우는 MLE가 아닌 Two sample tests라는 방법을 이용했기에 model architectures를 선택하는 데 있어 flexibility를 갖고 있지만, likelihood를 evaluation 할 수 없어(intractable) training 하기가 까다롭다. 또한 sampling시 다양한 sampling data가 아닌 특정 데이터만 자주 sampling 되는 mode collapse 문제도 갖고 있다. 이렇게 언급된 모든 단점을 극복하는 모델이 Energy-based models이다.

 

Parmeterizing probability distributions

Probability distribution $p(\mathbf{x})$를 모델링한다고 생각해 보자. 그럼 다음 두 가지의 조건을 만족해야 한다.

 

$$\begin{array}{rl}\text{Non-negativity}& :p(\mathbf{x})\ge 0\\ \text{Sum-to-one}& :\sum _{\mathbf{x}}p(\mathbf{x})=1\text{or}\int p(\mathbf{x})d\mathbf{x}=1\end{array}$$

 

임의의 함수 $f_{\theta}(\mathbf{x})$ 가 존재한다고 가정하자. 이때 이 함수가 첫 번째 조건인 Non-negativity를 만족하게 만드는 것은 매우 쉽다. 첫 번째 조건을 만족하도록 만든 함수를 $g_{\theta}(\mathbf{x})$ 라고 하면, 아래와 같이 다양하게 만들 수 있다.

 

$$\begin{array}{rl}& g_{\theta }(\mathbf{x})=f_{\theta }(\mathbf{x}{)}^2\\ & g_{\theta }(\mathbf{x})=\exp (f_{\theta }(\mathbf{x}))\\ & g_{\theta }(\mathbf{x})=|f_{\theta }(\mathbf{x})|\end{array}$$

 

이때 $g_{\theta}(\mathbf{x})$가 두 번째 조건인 Sum-to-one을 만족하지 않을 가능성이 있다. 그러므로 $g_{\theta}(\mathbf{x})$을 적분한 값을 나누어준다면 두 번째 조건을 만족하게 될 것이다. 이 과정을 통해 $p_{\theta}(\mathbf{x})$를 모델링하면 다음과 같이 쓸 수 있다.

 

$$p_{\theta }(\mathbf{x})=\frac{1}{Z(\theta )}{g}_{\theta }(\mathbf{x})=\frac{1}{\int g_{\theta }(\mathbf{x})d\mathbf{x}}{g}_{\theta }(\mathbf{x})$$

 

이렇게 $p_{\theta}(\mathbf{x})$를 모델링 했을때, $g_{\theta}(\mathbf{x})$가 항상 0보다 크거나 같기만 하다면 어떠한 모델이든 상관없다. 뒤에서 자세히 말하겠지만 실제로 모델을 선택하는 것을 $f_{\theta}$로 놓고 이를 항상 0보다 크거나 같게 만들어주어 $p_{\theta}(\mathbf{x})$를 모델링한다. 즉, Energy-based models는 model architectures를 선택하는데 있어 어떤 제약이 없다. 예를 들어 위에서 언급한 Autoregressive, Normalizing flow, VAE와 같은 모델을 $g_{\theta}(\mathbf{x})$로 설정해도 된다. 그렇기에 energy-based model이 위에 언급한 모델 대비 더 큰 범주라고 볼 수 있다.

 

Latent variables 모델 중 하나인 gaussian mixture 모델을 예시를 들어 $g_{\theta}(\mathbf{x})$가 높은 flexibility를 갖고 있음을 확인 해 보자. 2개의 multivariate gaussian function $G_{\theta}(\mathbf{x})$, $G_{\theta'}(\mathbf{x})$이 있다고 가정하자. 이때 prior로 $G_{\theta}(\mathbf{x})$를 선택할 확률을 $\alpha$라 하면, $G_{\theta'}(\mathbf{x})$를 선택할 확률은 $1 - \alpha$가 된다. 그럼 probability distribution $p_{\theta}(\mathbf{x})$를 다음과 같이 쓸 수 있다.

 

$$g_{\theta }(\mathbf{x})=\alpha G_{\theta }(\mathbf{x})+(1-\alpha )G_{{\theta }^{\prime }}(\mathbf{x})$$

 

이때 $g_{\theta}(\mathbf{x})$를 모든 $\mathbf{x}$에 대해 적분하면 1이 나오므로 $Z({\theta}) = 1$ 이므로  $p_{\theta}(\mathbf{x}) = g_{\theta}(\mathbf{x})$ 임을 확인할 수 있다. 이렇듯 $g_{\theta}(\mathbf{x})$는 다양한 모델이 가능하며 적분 값을 구할 수 있다면 $p_{\theta}(\mathbf{x})$를 모델링할 수 있다. 

 

Energy-based model

 

Energy-based model에서 정의하는 $p_{\theta}(\mathbf{x})$는 다음과 같다.

 

$$p_{\theta }(\mathbf{x})=\frac{1}{Z(\theta )}\exp (f_{\theta }(\mathbf{x}))=\frac{1}{\int \exp (f_{\theta }(\mathbf{x}))d\mathbf{x}}\exp (f_{\theta }(\mathbf{x}))$$

 

앞에 언급된 예시에 따르면 $g_{\theta}(\mathbf{x}) = \exp(f_{\theta}(\mathbf{x}))$를 선택한 것이다. 그럼 $\exp(f_{\theta}(\mathbf{x}))$는 $f_{\theta}(\mathbf{x})^{2}$와 같은 다른 가능한 함수들에 비해 어떠한 장점을 갖고 있을까? 먼저 $\exp$ 함수는 지수함수이기에 $\mathbf{x}$의 작은 변화를 잘 반영할 수 있다. 또, 기본적으로 최적화를 할 때, log-likelihood를 많이 이용하므로 $\exp$를 이용하면 $\log$를 취했을 때 $f_{\theta}(\mathbf{x})$만을 가지고 최적화를 진행할 수 있다. 게다가 gaussian distribution 같은 기본적이면서 간단한 분포들이 이러한 exponential 함수를 띈 경우가 많다.

 

그럼 이 모델의 이름에 왜 "Energy"가 들어가는 걸까? 이는 물리학에서 자주 사용하는 "Energy function"의 개념을 차용한 것이기 때문이다. 예를 들어 물리학에서 어떤 시스템에서 특정 상태 $x$에 있을 확률을 나타내는 Boltzmann Distribution은 다음과 같이 쓸 수 있다.

 

$$P(x)=\frac{1}{Z}\exp (-\frac{E(x)}{k_{B}T})$$

 

parameters에 대한 자세한 설명은 넘어가고 우리가 모델링한 $p_{\theta}(\mathbf{x})$를 보았을 때, 위의 식과 같은 모양임을 확인할 수 있다. 그래서 이 모델이 Energy-based models이라고 불린다.

 

Energy-based models은 다양한 model architectures를 선정할 수 있기에 큰 강점을 갖고 있지만, 치명적인 문제점을 갖고 있다. 바로 $Z({\theta})$를 구하기가 매우 까다롭다는 것이다. (tricky 하다고 한다.) $\exp(f_{\theta}(\mathbf{x}))$가 gaussian distribution처럼 간단한 함수라면 $Z({\theta})$ 값을 analytical하게 구할 수 있지만, neural networks처럼 복잡한 모델이라면 구하기가 어렵다. 두 가지 예시를 보면서 이를 확인해 보자.

 

먼저 $f_{\theta}{(x)} = -\frac{(x - {\mu})^{2}}{2{\sigma}^{2}}$으로 놓아서 1-D gaussian distribution을 생각해 보자.

 

$$Z(\theta )=\int \exp (f_{\theta }(x))dx=\int \exp (-\frac{(x-\mu {)}^2}{2{\sigma }^2})dx=\sqrt{2\pi {\sigma }^2}$$

 

위 식에서 볼 수 있다시피 gaussian distribution처럼 간단한 분포에 대해서는 analytical 하게 $Z({\theta})$ 값을 구할 수 있다. 반면, 모델이 복잡해지면 analytical하게 구하기 힘들어진다. $f_{\theta}{(\mathbf{x})}$를 Restricted Boltzmann Machine(RBM)으로 모델링하면 다음과 같이 쓸 수 있다.

 

$$\begin{array}{rl}& f_{\theta }(\mathbf{x})={\mathbf{x}}^{\text{T}}W\mathbf{z}+b\mathbf{x}+c\mathbf{z}\\ & P_{(W,b,c)}(\mathbf{x},\mathbf{z})=\frac{1}{Z}\exp ({\mathbf{x}}^{\text{T}}W\mathbf{z}+b\mathbf{x}+c\mathbf{z})\\ & \mathbf{x}\in \{0,1{\}}^n,\mathbf{z}\in \{0,1{\}}^m\end{array}$$

 

이 모델에서 $Z({\theta}) = Z(W, b, c)$ 값을 구하면 다음과 같다.

 

$$Z(W,b,c)=\sum _{\mathbf{x}\in \{0,1{\}}^n}\sum _{\mathbf{z}\in \{0,1{\}}^m}\exp ({\mathbf{x}}^{\text{T}}W\mathbf{z}+b\mathbf{x}+c\mathbf{z})$$

 

모든 $\mathbf{x}$, $\mathbf{z}$에 대한 합을 구해야 하므로 총 $2^{m+n}$의 경우에 대해 구해야 한다. 만약 $\mathbf{x}$가 MNIST와 같이 저화질 이미지(28x28)를 갖는 데이터라고 할지라도 n = 784가 되기에 $Z(W, b, c)$를 구하는 것은 사실상 불가능에 가깝다.

 

Pros and Cons

앞서 언급하였듯이 Energy-based models는 다양한 model architectures를 유용하게 사용할 수 있다는 점에서 큰 장점을 갖는다. 반면, 많은 경우 likelihood를 evaluation 하는 것이 불가능하다. 그렇기에 inference시에 $p_{\theta}(\mathbf{x})$를 기반으로 sampling 하는 것이 어렵고, training시에도 likelihood를 optimize 하는 것이 쉽지 않고 training을 멈춰야 하는 criterion을 설정하는 것이 어렵다.

 

Application of Energy-based models

그럼에도 불구하고 Energy-based models는 널리 쓰인다. 그 이유는 특정 task에 대해서는 $Z({\theta})$를 계산할 필요가 없기 때문이다. 예를 들어 $\mathbf{x}$, $\mathbf{x}'$가 주어져 있다고 가정하자. 이때 $p_{\theta}(\mathbf{x})$와 $p_{\theta}(\mathbf{x}')$의 상대적인 비율을 계산할 때는 $Z({\theta})$를 계산할 필요가 없다. 이를 수식으로 쓰면 다음과 같다.

 

$$\frac{p_{\theta }(\mathbf{x})}{p_{\theta }({\mathbf{x}}^{\prime })}=\exp (f_{\theta }(\mathbf{x})-f_{\theta }({\mathbf{x}}^{\prime }))$$

 

 $\mathbf{x}$가 $\mathbf{x}'$에 비해 얼마나 더 높은 확률을 갖고 있는지를 계산하고 싶을 때는 $Z({\theta})$를 계산할 필요가 없어진다.

 

Training

앞서 Energy-based models의 likelihood를 evaluation 하는 것이 어렵기에 training 하기가 쉽지 않다고 했는데, 그럼 어떻게 training 할 수 있을까? 1개의 train data $\mathbf{x}_{train}$이 있다고 생각해 보자. MLE를 통해 최적화를 한다고 했을 때, 우리는 $p_{\theta}(\mathbf{x}_{train})$ 값이 최대가 되길 원한다. 그러므로 아래와 같이 쓸 수 있다.

 

$$\text{Goal:}max{p}_{\theta }({\mathbf{x}}_{train})=max\frac{\exp (f_{\theta }({\mathbf{x}}_{train}))}{Z(\theta )}$$

 

모델의 parameters $\theta$를 업데이트할 때, 분자는 커지고 분모는 작아진다면 $p_{\theta}(\mathbf{x}_{train})$ 값이 커지므로 우리가 원하는 모델에 가까워질 것이다. 하지만 여기서 문제점이 만약 분자만 고려하여 $\theta$를 업데이트한다면 분자는 커지겠지만, 동시에 분모인 $Z({\theta})$ 값도 커져서 $p_{\theta}(\mathbf{x}_{train})$이 작아질 수도 있다. 그렇기에 우리는 training시 $\theta$가 분모, 분자 모두에 영향을 미친다는 것을 유념해야 한다.

 

Contrastive Divergence

그렇다면 우리는 $Z({\theta})$ 값을 얻을 수 없는데 어떻게 likelihood를 maximize 할 수 있을까? log-likelihood의 gradient를 구하는 수식을 보면 알 수 있다.

 

$$\begin{array}{rl}\text{log-likelihood}& :\log p_{\theta }({\mathbf{x}}_{train})=f_{\theta }({\mathbf{x}}_{train})-\log Z(\theta )\\ \text{Maximize}& :\underset{\theta }{max}{f}_{\theta }({\mathbf{x}}_{train})-\log Z(\theta )\end{array}$$

$$\begin{array}{r}\text{Gradient of log-likelihood:}\\ & {\mathrm{\nabla }}_{\theta }{f}_{\theta }({\mathbf{x}}_{train})-{\mathrm{\nabla }}_{\theta }\log Z(\theta )\\ =& {\mathrm{\nabla }}_{\theta }{f}_{\theta }({\mathbf{x}}_{train})-\frac{{\mathrm{\nabla }}_{\theta }Z(\theta )}{Z(\theta )}\\ =& {\mathrm{\nabla }}_{\theta }{f}_{\theta }({\mathbf{x}}_{train})-\frac{1}{Z(\theta )}\int {\mathrm{\nabla }}_{\theta }\exp (f_{\theta }(\mathbf{x}))d\mathbf{x}\\ =& {\mathrm{\nabla }}_{\theta }{f}_{\theta }({\mathbf{x}}_{train})-\frac{1}{Z(\theta )}\int \exp (f_{\theta }(\mathbf{x})){\mathrm{\nabla }}_{\theta }{f}_{\theta }(\mathbf{x})d\mathbf{x}\\ =& {\mathrm{\nabla }}_{\theta }{f}_{\theta }({\mathbf{x}}_{train})-\int \frac{\exp (f_{\theta }(\mathbf{x}))}{Z(\theta )}{\mathrm{\nabla }}_{\theta }{f}_{\theta }(\mathbf{x})d\mathbf{x}\\ =& {\mathrm{\nabla }}_{\theta }{f}_{\theta }({\mathbf{x}}_{train})-{\mathbf{E}}_{{\mathbf{x}}_{sample}\sim p_{\theta }}[{\mathrm{\nabla }}_{\theta }{f}_{\theta }({\mathbf{x}}_{sample})]\\ \approx & {\mathrm{\nabla }}_{\theta }{f}_{\theta }({\mathbf{x}}_{train})-{\mathrm{\nabla }}_{\theta }{f}_{\theta }({\mathbf{x}}_{sample})\end{array}$$

 

식 자체는 크게 어렵지 않으니, 자세한 유도과정에 대한 설명은 생략하겠다. 마지막 부분에 expectation 부분의 $\mathbf{x}_{sample}$은 $p_{\theta}$에서 샘플링한 것이다. Monte Carlo Estimation을 통해 expectation 값을 구하면 $p_{\theta}$에서 $N$개를 sampling 하여 평균을 내야하지만, $p_{\theta}$에서 sampling하는 과정이 까다롭기 때문에 1개만 sampling하여 얻은 값으로 approximation($\nabla_{\theta}f_{\theta}(\mathbf{x}_{sample}$))한 것을 볼 수 있다.

 

Gradient 수식에서 마지막 식의 의미를 살펴보자. 우리는 $\max \frac{\exp(f_{\theta}(\mathbf{x}_{train}))}{Z({\theta})}$를 위해 log-likelihood의 gradient인 $\nabla_{\theta}f_{\theta}(\mathbf{x}_{train}) - \nabla_{\theta}\log Z({\theta})$ 를 구했고, 수식을 정리한 결과 $\nabla_{\theta}f_{\theta}(\mathbf{x}_{train}) - \nabla_{\theta}f_{\theta}(\mathbf{x}_{sample})$를 얻었다. 즉, 이 gradient 방향으로 gradient ascent를 수행하면 $\exp(f_{\theta}(\mathbf{x}_{train}))$는 커지고 $Z({\theta})$ 값은 작아질 것이다. 여기서 우리가 $Z({\theta})$의 값을 모르는데 training이 가능한 이유는 $\log Z({\theta})$의 gradient 값을 $\nabla_{\theta}f_{\theta}(\mathbf{x}_{sample})$를 통해 구할 수 있기 때문이다. 즉, $p_{\theta}$에서 sampling만 할 수 있다면 $\log Z({\theta})$를 계산할 수 없어도 training이 가능하단 것이다! 또 마지막 수식을 생각해 보면 train data에 대해서는 $f_{\theta}$ 값을 크게 만들고 $\mathbf{x}_{sample}$에 대해서는 $f_{\theta}$의 값을 작게 만든다. $\exp (f_{\theta})$는 pdf 함수이기 때문에 $f_{\theta}$ 또한 pdf 함수로 볼 수 있다. $\mathbf{x}_{sample}$의 $f_{\theta}$ 값을 작게 만든다는 것은 train data 이외 sampling 한 데이터는 모두 noise data 또는 wrong data로 보겠다는 말과 동치라고 생각할 수 있다. 이를 그래프로 나타내면 아래와 같다.

Figure 1. EBM training process (출처: Stanford CS236, lecture 11)

 

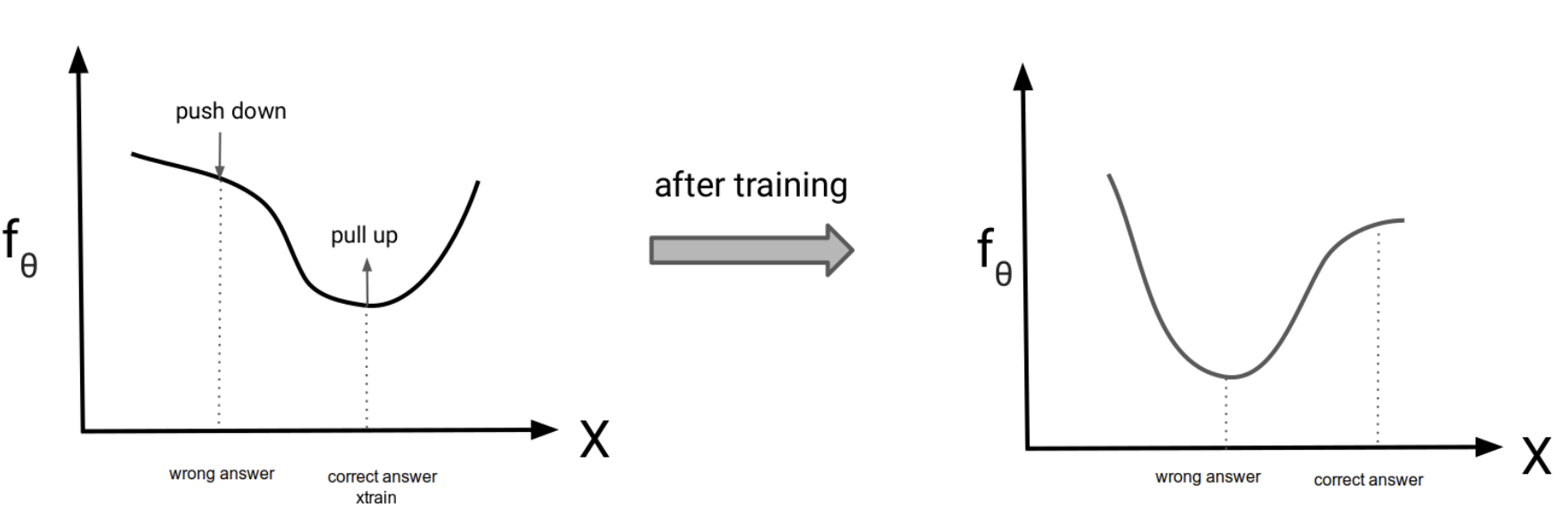
Figure 1은 Energy-based models의 training 과정을 그래프로 나타낸 것이다. 여기서 wrong answer은 $\mathbf{x}_{sample}$로 생각할 수 있다.

 

How to Sample from  $P_{\theta}$?

$\log Z({\theta})$의 gradient는 $\mathbf{x}_{sample}$를 통해 구할 수 있다. 하지만 여기서도 문제점이 있다. Likelihood인 $p_{\theta}$를 evaluate할 수 없는데, 어떻게 $p_{\theta}$에서 $\mathbf{x}_{sample}$를 sampling 할 수 있을까?

 

Metropolis-Hastings Markov Chain Monte Carlo (MH-MCMC)

MH-MCMC는 임의의 분포 $\pi(\mathbf{x})$에서 sampling 한 $\mathbf{x}$를 $p_{\theta}$에서 sampling한 것처럼 만들어주는 과정이라고 생각하면 된다. 이때 likelihood를 evaluation 하는 것이 아닌 $f_{\theta}$를 이용한다. 알고리즘은 다음과 같다.

 

$$\begin{array}{rl}& {\mathbf{x}}^{(0)}\sim \pi (\mathbf{x})\\ & \text{Repeat for }t=0,1,2,\dots T-1:\\ & {\mathbf{x}}^{\prime }={\mathbf{x}}^{(t)}+\text{noise}\\ & \text{if}{f}_{\theta }({\mathbf{x}}^{\prime })\ge f_{\theta }({\mathbf{x}}^{(t)}),{\mathbf{x}}^{(t+1)}={\mathbf{x}}^{\prime }\\ & \text{if}{f}_{\theta }({\mathbf{x}}^{\prime })<f_{\theta }({\mathbf{x}}^{(t)}),\\ & \text{set}{\mathbf{x}}^{(t+1)}={\mathbf{x}}^{\prime }\text{with probability}\exp (f_{\theta }({\mathbf{x}}^{\prime })-f_{\theta }({\mathbf{x}}^{(t)}))\\ & \text{otherwise,}\text{set}{\mathbf{x}}^{(t+1)}={\mathbf{x}}^{(t)}\end{array}$$

 

먼저 $\mathbf{x}^{(0)}$를 임의의 분포 $\pi(\mathbf{x})$에서 sampling 한다. 이후 noise를 더해 새로운 sample $\mathbf{x}'$을 만들고 두 개의 $f_{\theta}$ 값을 비교하여, 후자가 더 크다면 2번째 데이터로 $\mathbf{x}'$를 선택한다. 만약 후자가 더 작다면 $\exp(f_{\theta}(\mathbf{x}') - f_{\theta}(\mathbf{x}^{(0)})$의 확률로 2번째 데이터로 $\mathbf{x}'$ 선택되게 만든다. 이 과정을 $T$번 계속해서 반복하면 $\mathbf{x}^{(T)} \sim p_{\theta}$로 근사할 수 있다. 

 

여기서 $f_{\theta}(\mathbf{x}') \geq f_{\theta}(\mathbf{x}^{(t)})$ 일 경우엔 $\mathbf{x}'$ 의 likelihood 값이 더 클 가능성이 높기에 $\mathbf{x}^{(t+1)}$ 로 $\mathbf{x}'$를 이용하는 것이 이해가 되는데, 반대의 경우인 $f_{\theta}(\mathbf{x}') < f_{\theta}(\mathbf{x}^{(t)})$엔 왜 바로 알고리즘을 멈추지 않고 더 낮은 $f_{\theta}$를 갖는 $\mathbf{x}'$ 가 $\mathbf{x}^{(t+1)}$ 될 수 있는 확률을 부여하는 걸까? 이는 local maxima 값을 탈출하기 위한 기회를 주는 것이라 생각하면 된다. 현재 우리가 집중하고 있는 것은 "Optimize"가 아닌 "Sampling"이다. 그러므로 높은 $f_{\theta}$ 값을 갖는 sample을 갖는 것이 중요하지만 항상 local maxima에 있는 sample 갖길 원하는 것은 아니다. 우리는 다양한 wrong sample로부터 gradient를 구해야 하기 때문이다. 또한 이 알고리즘이 $\mathbf{x}^{(T)} \sim p_{\theta}$을 만족하게 하는 이유는 이 알고리즘이 detailed balance condition을 만족하기 때문이다. 이에 대한 설명은 글이 너무 길어지는 관계로 생략하겠다. 여기서 중요한 점은 $T$가 굉장히 큰 수라는 것이다. 즉, 1개의 sample을 얻는데 시간이 매우 오래 걸리기에 MLE로 training시 local maxima까지 도달하는데 시간 또한 오래 걸린다.

 

Unadjusted Langevin MCMC

이 방법은 위 MH-MCMC와 유사한 알고리즘을 갖고 있다. 다만 여기선 sampling 할 때, $f_{\theta}$ 값을 evaluation 하지 않는다. 알고리즘은 아래와 같다. 

 

$$\begin{array}{rl}& {\mathbf{x}}^{(0)}\sim \pi (\mathbf{x})\\ & \text{Repeat for }t=0,1,2,\dots T-1:\\ & {\mathbf{z}}^{(t)}\sim \mathcal{N}(0,I)\\ & {\mathbf{x}}^{(t+1)}={\mathbf{x}}^{(t)}+ϵ{\mathrm{\nabla }}_{\mathbf{x}}\log p_{\theta }(\mathbf{x}){|}_{\mathbf{x}={\mathbf{x}}^t}+\sqrt{2ϵ}{\mathbf{z}}^{(t)}\end{array}$$

 

Energy-based models에서 $\nabla_{\mathbf{x}} \log p_{\theta}(\mathbf{x}) = \nabla_{\mathbf{x}} f_{\theta}(\mathbf{x})$이기 때문에 $\mathbf{x}$ 값은 log-likelihood 값이 증가하는 방향으로 업데이트된다. 여기서 $\epsilon$은 step size로 보면 된다. MH-MCMC에서 무조건 local maxima에서 sampling 되는 것을 방지하기 위해 했던 것처럼 여기서는 gaussian distribution에서 sampling 한 $\mathbf{z}$ 값을 추가하여 전체 space를 다양하게 탐색하게 한다. 그래서 결과적으로 임의의 분포에서 sampling 한 $\mathbf{x}$ 값을 $\mathbf{x} \sim p_{\theta}$로 만든다. 하지만 이 방법도 문제는 1개의 sample을 얻기 위해 매우 많은 iteration이 필요하다는 것이다. 또한 gradient를 계산해야 하기에 차원이 커짐에 따라 계산량도 증가하다는 단점이 있다.

 

Summary

Energy-based models는 물리학에서 자주 사용하는 energy function을 기반으로 하여 확률을 모델링한다. 그 결과 다양한 model architectures를 선택할 수 있다는 장점을 갖지만, likelihood를 evaluation을 평가할 수 없다는 치명적인 단점 또한 가진다. Training시에는 다행히 $Z(\theta)$ 값을 알지 못해도 $p_\theta$에서 sampling 한 데이터를 갖고 training을 할 수 있다. 하지만 sampling 하는 것 역시 likelihood가 intractable 하다는 특징 때문에 직접 sampling 하는 것이 아닌 MH-MCMC 혹은 unadjusted Langevin MCMC처럼 시간이 오래 걸리는 방법을 써야 한다. 다음 주제에선 이러한 inefficient 한 sampling 방법을 벗어난 Training without sampling 방법을 설명할 예정이다.

 

Reference

[1] Stanford CS236, lecture 11